人教七年级数学上册2.2.2 有理数的除法（第2课时 有理数的加减乘除混合运算）课件含教案PPT

这份PowerPoint由四个部分构成。第一部分内容是复习导入，该部分引导学生联系新旧知识。第二部分内容是新课探究，这一部分首先展示了教科书中的例题，其次介绍了列表法和连线法，最后对排列与组合的区别进行简要说明。第三部分内容是随堂练习和培优训练，这一部分主要包括《做一做》、《选一选》、《算一算》。第四部分内容是课堂小结和课后作业。

PPT课件从四个部分来展开介绍关于人教版一年级上册数学课程《6和7的分与合》第二课时的教学内容。PPT课件的第一部分通过提问的方式来导入课程，充分激发了学生的求知欲。第二部分借助小红花和小方块等具体事物来引导学生探究6和7的分与合，并引导学生完成了相关练习题目。第三部分展示了有关《6和7的分与合》的培优训练题。第四部分总结归纳了本节课的重点内容。

这份演示文稿主要从四个部分对图形的旋转第二课时进行详细展开。首先是探究新知，这一部分主要介绍了平移和旋转的相同点和不同点。第二部分介绍了利用旋转设计图案的方式，同时还展示了中考有关图形旋转的真题。第三部分是课堂检测部分，主要检测教师的教学效果和学生的学习情况。第四部分是课堂小结和课后作业的相关内容展示。

PPT课件从四个部分来展开介绍关于人教版九年级上册数学课程《直线和圆的位置关系》第二课时的教学内容。PPT课件的第一部分阐述了本节课的三点素养目标。第二部分介绍了切线的含义，并探究了判定切线的三个判定方法。第三部分详细地介绍了切线的性质定理以及其应用格式。第四部分展示了各种题型的练习题目，并通过思维导图的形式归纳了本节课的重点内容。

这份PPT由四个部分组成。第一部分内容是素养目标，此模板首先要了解“SSA”不能作为两个三角形全等的条件，其次会用“SAS”判定条件证明两个三角形全等并能运用其解决实际问题，最后能够正确理解三角形全等的判定定理。第二部分内容是探究新知，这一部分主要包括“边角边”定理和判定方法、利用全等三角形测距离、三角形全等条件的识别。第三部分内容是链接中考。第四部分内容是课堂检测和课堂小结。

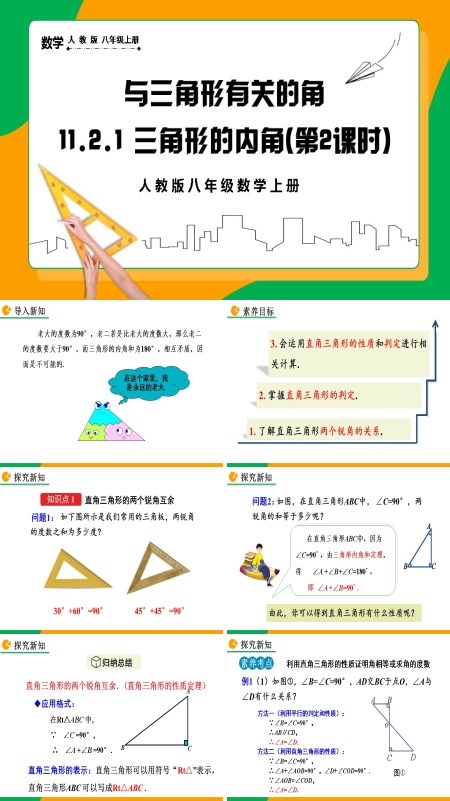
这份PPT由四个部分组成。第一部分内容是导入新知和目标素养。第二部分内容是探究新知，这一部分首先展示了与直角三角形的两个锐角相关的两个问题，其次对直角三角形的性质定理进行归纳总结，最后展示了与直角三角形性质有关的考点。第三部分内容是巩固练习，这一部分主要展示了三道习题。第四部分内容是链接中考和课堂检测，其中包括基础巩固题和能力提升题。

这份PPT由四个部分组成。第一部分内容是新课探究，此模板首先引导学生玩有关新知识的小游戏，其次是对游戏规则进行介绍，最后引出所学新知识。第二部分内容是随堂练习，这一部分主要包括《填一填》、《算一算》。第三部分内容是课后练习，这一部分一方面展示了三道基础巩固题，另一方面是对四道能力提升题进行展示。第四部分内容是课堂小结。

这份PowerPoint由五个部分构成。第一部分内容是教学内容、目标和重难点。第二部分内容是探究、建构事件的包含关系的定义，这一部分首先介绍了事件的关系，其次是事件的运算，最后对强化概念解决问题进行介绍。第三部分内容是课堂小结，凝练升华，这一部分首先引导学生回顾本节课的知识内容，其次要求学生回答相关问题，最后展示设计意图。第四部分内容是课堂检测与评价。第五部分内容是教学反思。

该课件以幻灯片的形式对地形图的判读进行了简要的回顾，方便主讲老师在使用PowerPoint时更好的带领同学进行复习。PPT课件的第一部分是知识回顾，介绍了一些具体山体部位的名称及地形图。第二部分是认识地形，介绍了地形的概念、山地的特点、丘陵的特点、高原的特点、盆地的特点、平原的特点等内容，并呈现了相关的图片。第三部分是分层设色地形图，介绍了分层色地形图的概念以及各种颜色所表示的地形。此外，这一部分还介绍了安第斯山脉、刚果盆地、亚马逊平原、青藏高原等内容。

该课件以幻灯片的形式介绍了地球的公转的内容，方便主讲老师在使用PowerPoint时更好的介绍地球公转的意义。PPT课件的第一部分是地球公转的基本特征，介绍了地球公转的运动方向、旋转中心及周期。第二部分是四季，介绍了春分、夏至、秋分、冬至等内容。第三部分是昼夜长短的变化，介绍了昼夜长短的判断方法、极昼极夜现象的成因、昼夜长短随季节的变化规律等内容。第四部分是五带，介绍了公转产生的地理现象、五带的划分、五带的气候特征等内容。

本套PPT课件专为人教版数学八年级下册勾股定理的第一课时设计，共31张幻灯片，旨在帮助学生深入理解勾股定理的内涵，掌握其表达方式，并能够灵活运用勾股定理解决实际问题。通过本课程的学习，学生将形成数形结合的思维方式，并在逻辑推理能力上得到显著提升。 课程内容分为四个部分，全面而系统地介绍了勾股定理的相关知识。第一部分为探究新知，通过直角三角形的实例，引导学生探索不同三角形之间的关系，自然引出勾股定理的主题。这一部分激发学生的好奇心和探究欲，为后续的学习打下基础。 第二部分为新知讲解，通过几何画板软件的直观展示，结合古人赵爽的证法、毕达哥拉斯证法以及加菲尔德的“总统证法”，深入总结勾股定理的几何意义、符号表示和公式变形。这一部分不仅让学生了解勾股定理的历史背景，还通过多种证法增强学生对定理的理解。 第三部分为典例分析，通过具体的例题讲解，明确解题过程和步骤，帮助学生加深对勾股定理知识点的理解和应用。这一部分通过实践操作，让学生将理论知识转化为解题技能。 第四部分为课堂小结，采用思维导图的形式，帮助学生梳理和总结本节课的知识点。这一部分通过视觉化的工具，让学生对勾股定理有一个清晰的认识，加深记忆。 整个课件的设计注重从直观到抽象的过渡，通过历史证法和现代软件的结合，帮助学生全面理解勾股定理。同时，通过丰富的例题和思维导图的总结，提高学生的解题能力和知识整合能力。这样的教学安排不仅有助于学生掌握勾股定理，还能培养他们的数学思维和解决问题的能力，为未来的数学学习奠定坚实的基础。通过这一系列的教学活动，学生将在实际问题中灵活运用勾股定理，提高他们的数学素养和逻辑推理能力。

本课件旨在为二年级下册数学课程中关于有余数的除法单元提供一个全面的复习。课件共包含30张幻灯片，旨在帮助学生熟练掌握有余数除法的计算技巧，并深刻理解余数的概念，以及如何将这些知识应用于解决实际问题。通过这一复习过程，我们期望学生能够提升他们的计算技能和问题解决能力。 课件的第一部分聚焦于有余数除法的计算。通过梳理关键知识点和解析难点，本部分旨在帮助学生回顾有余数除法的基本概念，包括余数与除数之间的联系、笔算除法的步骤以及如何使用竖式试商方法进行计算。这一部分不仅涵盖了理论知识，还通过实例演示了如何应用这些知识。 第二部分则转向实际问题解决。通过一系列精心设计的习题，学生将有机会将所学知识应用于实际情境中，从而加深对有余数除法的理解，并提高他们解决实际问题的能力。这些习题覆盖了从基础到进阶的不同难度，确保所有学生都能在适合自己的水平上得到练习。 整个课件的设计旨在通过互动和实践，使学生能够构建起一个完整的知识体系，不仅理解有余数除法的计算方法，还能掌握如何灵活运用这些方法来解决各种问题。通过这样的复习，学生将能够在数学学习中取得更大的进步，为未来的学习打下坚实的基础。

本节PPT课件旨在引导学生深入理解并掌握二次根式的乘法规则，通过33张幻灯片的丰富内容，全面提升学生的运算技巧和逻辑推理能力，同时培养他们严谨的学习态度。课程内容分为十个部分，全面覆盖了二次根式乘法的各个方面。 首先，通过情景导入部分激发学生兴趣，引出本课主题。接着，新知探究环节通过具体的二次根式乘法例子，引导学生自主发现并总结乘法法则。新知运用部分则通过实际计算，展示如何应用这些法则，并强调结果必须化简至最简形式，同时注重书写的规范性。 新知讲解部分明确提出“积的算术平方根等于各因式算术平方根的积”这一核心概念。典例讲解和变式训练部分则通过具体的计算题目，帮助学生巩固对乘法法则的理解和应用。拓展探究部分进一步深化学生对知识点的理解。 当堂检测环节让学生即时检验自己的学习成果，而小结梳理部分则帮助学生回顾和总结本节课的重点内容。最后，布置作业部分为学生提供了课后练习，以巩固课堂所学。 通过这一系列的教学活动，学生不仅能够掌握二次根式的乘法法则，还能在实际问题中灵活运用，从而提高他们的数学素养和解决问题的能力。本课件的设计注重理论与实践相结合，旨在通过多样化的教学手段，使学生在轻松愉快的氛围中掌握数学知识，为后续更复杂的数学学习打下坚实的基础。

该PPT课件以幻灯片的形式介绍了同分母分数的加、减的内容，方便教师在使用PowerPoint 时更好的介绍分数的基本性质。在授课过程中，教师可以通过贴近学生生活的实例，引出同分母分数的加减法问题。第一部分通过举例子进行复习导入。第二部分进行新课探究，通过分析教科书上的例子，总结同分母分数的加、减法相关规律。第三部分进行随堂练习，完成教科书上的相关练习。第四部分进行培优训练，帮助灵活运用本堂所学知识点。第五部分总结本课要点，并布置课后作业。